Ice Lake Store Elimination
Introduction
If you made it down to the hardware survey on the last post, you might have wondered where Intel’s newest mainstream architecture was. Ice Lake was missing!
Well good news: it’s here… and it’s interesting. We’ll jump right into the same analysis we did last time for Skylake client. If you haven’t read the first article you’ll probably want to start there, because we’ll refer to concepts introduced there without reexplaining them here.
As usual, you can skip to the summary for the bite sized version of the findings.
ICL Results
The Compiler Has an Opinion
Let’s first take a look at the overall performance: facing off fill0 vs fill1 as we’ve been doing for every microarchitecture. Remember, fill0 fills a region with zeros, while fill1 fills a region with the value one (as a 4-byte int).
All of these tests run at 3.5 GHz. The max single-core turbo for this chip is at 3.7 GHz, but is difficult to run in a sustained manner at this frequency, because of AVX-512 clocking effects and because other cores occasionally activate. 3.5 GHz is a good compromise that keeps the chip running at the same frequency, while remaining close to the ideal turbo. Disabling turbo is not a good option, because this chip runs at 1.1 GHz without turbo, which would introduce a large distortion when exercising the uncore and RAM.
Actually, I lied. This is the right plot for Ice Lake:
Well, which is it?
Those two have a couple of key differences. The first is this weird thing that Figure 7a has going on in the right half of the L1 region: there are two obvious and distinct performance levels visible, each with roughly half the samples.
The second thing is that while both of the plots show some of the zero optimization effect in the L3 and RAM regions, the effect is much larger in Figure 7b:
So what’s the difference between these two plots? The top one was compiled with -march=native, the second with -march=icelake-client.
Since I’m compiling this on the Ice Lake client system, I would expect these to do the same thing, but for some reason they don’t. The primary difference is that -march=native generates 512-bit instructions like so (for the main loop):
.L4:
vmovdqu32 [rax], zmm0
add rax, 512
vmovdqu32 [rax-448], zmm0
vmovdqu32 [rax-384], zmm0
vmovdqu32 [rax-320], zmm0
vmovdqu32 [rax-256], zmm0
vmovdqu32 [rax-192], zmm0
vmovdqu32 [rax-128], zmm0
vmovdqu32 [rax-64], zmm0
cmp rax, r9
jne .L4
Using -march=icelake-client uses 256-bit instructions1:
.L4:
vmovdqu32 [rax], ymm0
vmovdqu32 [rax+32], ymm0
vmovdqu32 [rax+64], ymm0
vmovdqu32 [rax+96], ymm0
vmovdqu32 [rax+128], ymm0
vmovdqu32 [rax+160], ymm0
vmovdqu32 [rax+192], ymm0
vmovdqu32 [rax+224], ymm0
add rax, 256
cmp rax, r9
jne .L4
Most compilers use 256-bit instructions by default even for targets that support AVX-512 (reason: downclocking, so the -march=native version is the weird one here. All of the earlier x86 tests used 256-bit instructions.
The observation that Figure 7a results from running 512-bit instructions, combined with a peek at the data lets us immediately resolve the mystery of the bi-modal behavior.
Here’s the raw data for the 17 samples at a buffer size of 9864:
| GB/s | |||
|---|---|---|---|
| Size | Trial | fill0 | fill1 |
| 9864 | 0 | 92.3 | 92.0 |
| 1 | 91.9 | 91.9 | |
| 2 | 91.9 | 91.9 | |
| 3 | 92.4 | 92.2 | |
| 4 | 92.0 | 92.3 | |
| 5 | 92.1 | 92.1 | |
| 6 | 92.0 | 92.0 | |
| 7 | 92.3 | 92.1 | |
| 8 | 92.2 | 92.0 | |
| 9 | 92.0 | 92.1 | |
| 10 | 183.3 | 93.9 | |
| 11 | 197.3 | 196.9 | |
| 12 | 197.3 | 196.6 | |
| 13 | 196.6 | 197.3 | |
| 14 | 197.3 | 196.6 | |
| 15 | 196.6 | 197.3 | |
| 16 | 196.6 | 196.6 | |
The performance follows a specific pattern with respect to the trials for both fill0 and fill1: it starts out slow (about 90 GB/s) for the first 9-10 samples then suddenly jumps up the higher performance level (close to 200 GB/s). It turns out this is just voltage and frequency management biting us again. In this case there is no frequency change: the raw data has a frequency column that shows the trials always run at 3.5 GHz. There is only a voltage change, and while the voltage is changing, the CPU runs with reduced dispatch throughput2.
The reason this effect repeats for every new set of trials (new buffer size value) is that each new set of trials is preceded by a 100 ms spin wait: this spin wait doesn’t run any AVX-512 instructions, so the CPU drops back to the lower voltage level and this process repeats. The effect stops when the benchmark moves into the L2 region, because there it is slow enough that the 10 discarded warmup trials are enough to absorb the time to switch to the higher voltage level.
We can avoid this problem simply by removing the 100 ms warmup (passing --warmup-ms=0 to the benchmark), and for the rest of this post we’ll discuss the no-warmup version (we keep the 10 warmup trials and they should be enough).
Elimination in Ice Lake
So we’re left with the second effect, which is that the 256-bit store version shows very effective elimination, as opposed to the 512-bit version. For now let’s stop picking favorites between 256 and 512 (push that on your stack, we’ll get back to it), and just focus on the elimination behavior for 256-bit stores.
Here’s the closeup of the L3 region for the 256-bit store version, showing also the L2 eviction type, as discussed in the previous post:
We finally have the elusive (near) 100% elimination of redundant zero stores! The fill0 case peaks at 96% silent (eliminated3) evictions. Typical L3 bandwidth is ~59 GB/s with elimination and ~42 GB/s without, for a better than 40% speedup! So this is a potentially a big deal on Ice Lake.
Like last time, we can also check the uncore tracker performance counters, to see what happens for larger buffers which would normally write back to memory.
Note: the way to interpret the events in this plot is the reverse of the above: more uncore tracker writes means less elimination, while in the earlier chart more silent writebacks means more elimination (since every silent writeback replaces a non-silent one).
As with the L3 case, we see that the store elimination appears 96% effective: the number of uncore to memory writebacks flatlines at 4% for the fill0 case. Compare this to Figure 3, which is the same benchmark running on Skylake-S, and note that only half the writes to RAM are eliminated.
This chart also includes results for the alt01 benchmark. Recall that this benchmark writes 64 bytes of zeros alternating with 64 bytes of ones. This means that, at best, only half the lines can be eliminated by zero-over-zero elimination. On Skylake-S, only about 50% of eligible (zero) lines were eliminated, but here we again get to 96% elimination! That is, in the alt01 case, 48% of all writes were eliminated, half of which are all-ones and not eligible.
The asymptotic speedup for the all zero case for the RAM region is less than the L3 region, at about 23% but that’s still not exactly something to sneeze at. The speedup for the alternating case is 10%, somewhat less than half the benefit of the all zero case4. In the L3 region, we also note that the benefit of elimination for alt01 is only about 7%, much smaller than the ~20% benefit you’d expect if you cut the 40% benefit the all-zeros case sees. We saw a similar effect in Skylake-S.
Finally it’s worth noting this little uptick in uncore writes in the fill0 case:
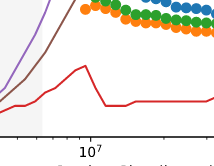
This happens right around the transition from L3 to RAM, and this, the writes flatline down to 0.04 per line, but this uptick is fairly consistently reproducible. So there’s some interesting effect there, probably, perhaps related to the adaptive nature of the L3 caching5.
512-bit Stores
If we rewind time, time to pop the mental stack and return to something we noticed earlier: that 256-bit stores seemed to get superior performance for the L3 region compared to 512-bit ones.
Remember that we ended up with 256-bit and 512-bit versions due to unexpected behavior in the -march flag. Rather they relying on this weirdness6, let’s just write slighly lazy7 methods that explicitly use 256-bit and 512-bit stores but are otherwise identical. fill256_0 uses 256-bit stores and writes zeros, and I’ll let you pattern match the rest of the names.
Here’s how they perform on my ICL hardware:
This chart shows only the the median of 17 trials. You can look at the raw data for an idea of the trial variance, but it is generally low.
In the L1 region, the 512-bit approach usually wins and there is no apparent difference between writing 0 or 1 (the two halves of the moon mostly line up). Still, 256-bit stores are roughly competitive with 512-bit: they aren’t running at half the throughput. That’s thanks to the second store port on Ice Lake. Without that feature, you’d be limited to 112 GB/s at 3.5 GHz, but here we handily reach ~190 GB/s with 256-bit stores, and ~195 GB/s with 512-bit stores. 512-bit stores probably have a slight advantage just because of fewer total instructions executed (about half of the 256-bit case) and associated second order effects.
Ice Lake has two store ports which lets it execute two stores per cycle, but only a single cache line can be written per cycle. However, if two consecutive stores fall into the same cache line, they will generally both be written in the same cycle. So the maximum sustained throughput is up to two stores per cycle, if they fall in the same line8.
In the L2 region, however, the 256-bit approaches seem to pull ahead. This is a bit like the Buffalo Bills winning the Super Bowl: it just isn’t supposed to happen.
Let’s zoom in:
The 256-bit benchmarks start roughly tied with their 512 bit cousins, but then steadily pull away as the region approaches the full size of the L2. By the end of the L2 region, they have nearly a ~13% edge. This applies to both fill256 versions – the zeros-writing and ones-writing flavors. So this effect doesn’t seem explicable by store elimination: we already know ones are not eliminated and, also, elimination only starts to play an obvious role when the region is L3-sized.
In the L3, the situation changes: now the 256-bit version really pulls ahead, but only the version that writes zeros. The 256-bit and 512-bit one-fill versions fall down in throughput, nearly to the same level (but the 256-bit version still seems slightly but measurably ahead at ~2% faster). The 256-bit zero fill version is now ahead by roughly 45%!
Let’s concentrate only on the two benchmarks that write zero: fill256_0 and fill512_0, and turn on the L2 eviction counters (you probably saw that one coming by now):
Only the L2 Lines Out Silent event is shown – the balance of the evictions are non-silent as usual.
Despite the fact that I had to leave the right axis legend just kind floating around in the middle of the plot, I hope the story is clear: 256-bit stores get eliminated at the usual 96% rate, but 512-bit stores are hovering at a decidedly Skylake-like ~56%. I can’t be sure, but I expect this difference in store elimination largely explains the performance difference.
I checked also the behavior with prefetching off, but the pattern is very similar, except with both approaches having reduced performance in L3 (you can see for yourself). It is interesting to note that for zero-over-zero stores, the 256-bit store performance in L3 is almost the same as the 512-bit store performance in L2! It buys you almost a whole level in the cache hierarchy, performance-wise (in this benchmark).
Normally I’d take a shot at guessing what’s going on here, but this time I’m not going to do it. I just don’t know9. The whole thing is very puzzling, because everything after the L1 operates on a cache-line basis: we expect the fine-grained pattern of stores made by the core, within a line to basically be invisible to the rest of the caching system which sees only full lines. Yet there is some large effect in the L3 and even in RAM10 related to whether the core is writing a cache line in two 256-bit chunks or a single 512-bit chunk.
Summary
We have found that the store elimination optimization originally uncovered on Skylake client is still present in Ice Lake and is roughly twice as effective in our fill benchmarks. Elimination of 96% L2 writebacks (to L3) and L3 writebacks (to RAM) was observed, compared to 50% to 60% on Skylake. We found speedups of up to 45% in the L3 region and speedups of about 25% in RAM, compared to improvements of less than 20% in Skylake.
We find that when zero-filling writes occur to a region sized for the L2 cache or larger, 256-bit writes are often significantly faster than 512-bit writes. The effect is largest for the L2, where 256-bit zero-over-zero writes are up to 45% faster than 512-bit writes. We find a similar effect even for non-zeroing writes, but only in the L2.
Future
It is an interesting open question whether the as-yet-unreleased Sunny Cove server chips will exhibit this same optimization.
Advice
Unless you are developing only for your own laptop, as of May 2020 Ice Lake is deployed on a microscopic fraction of total hosts you would care about, so the headline advice in the previous post applies: this optimization doesn’t apply to enough hardware for you to target it specifically. This might change in the future as Ice Lake and sequels roll out in force. In that case, the magnitude of the effect might make it worth optimizing for in some cases.
For fine-grained advice, see the list in the previous post.
Thanks
Vijay and Zach Wegner for pointing out typos.
Ice Lake photo by Marcus Löfvenberg on Unsplash.
Saagar Jha for helping me track down and fix a WebKit rendering issue.
Discussion and Feedback
If you have something to say, leave a comment below. There are also discussions on Twitter and Hacker News.
Feedback is also warmly welcomed by email or as a GitHub issue.
-
It’s actually still using the EVEX-encoded AVX-512 instruction
vmovdqu32, which is somewhat more efficient here because AVX-512 has more compact encoding of offsets that are a multiple of the vector size (as they usually are). ↩ -
In this case, the throughput is only halved, versus the 1/4 throughput when we looked at dispatch throttling on SKX, so based on this very preliminary result it seems like the dispatch throttling might be less severe in Ice Lake (this needs a deeper look: we never used stores to test on SKX). ↩
-
Strictly speaking, a silent writeback is a sufficient, but not a necessary condition for elimination, so it is a lower bound on the number of eliminated stores. For all I know, 100% of stores are eliminated, but out of those 4% are written back not-silently (but not in a modified state). ↩
-
One reason could be that writing only alternating lines is somewhat more expensive than writing half the data but contiguously. Of course this is obviously true closer to the core, since you touch half the number of the pages in the contiguous case, need half the number of page walks, prefetching is more effective since you cross half as many 4K boundaries (prefetch stops at 4K boundaries) and so on. Even at the memory interface, alternating line writes might be less efficient because you get less benefit from opening each DRAM page, can’t do longer than 64-byte bursts, etc. In a pathological case, alternating lines could be half the bandwidth if the controller maps alternating lines to alternating channels, since you’ll only be accessing a single channel. We could try to isolate this effect by trying more coarse grained interleaving. ↩
-
The L3 is capable of determining if the current access pattern would be better served by something like an MRU eviction strategy, for example when a stream of data is being accessed without reuse, it would be better to kick that data out of the cache quickly, rather than evicting other data that may be useful. ↩
-
After all, there’s a good chance it will be fixed in a later version of gcc. ↩
-
These are lazy in the sense that I don’t do any scalar head or tail handling: the final iteration just does a full width SIMD store even if there aren’t 64 bytes left: we overwrite the buffer by up to 63 bytes. We account for this when we allocate the buffer by ensuring the allocation is oversized by at least that amount. This doesn’t matter for larger buffers, but it means this version will get a boost for very small buffers versus approaches that do the fill exactly. In any case, we are interested in large buffers here. ↩
-
Most likely, the L1 has a single 64 byte wide write port, like SKX, and the commit logic at the head of the store buffer can look ahead one store to see if it is in the same line in order to dequeue two stores in a single cycle. Without this feature, you could execute two stores per cycle, but only commit one, so the long-run store throughput would be limited to one per cycle. ↩
-
Well I lied. I at least have some ideas. It may be that the CPU power budget is dynamically partitioned between the core and uncore, and with 512-bit stores triggering the AVX-512 power budget, there is less power for the uncore and it runs at a lower frequency (that could be checked). This seems unlikely given that it should not obviously affect the elimination chance. ↩
-
We didn’t take a close look at the effect in RAM but it persists, albeit at a lower magnitude. 256-bit zero-over-zero writes are about 10% faster than 512-bit writes of the same type. ↩
Comments
Hi Travis,
Re: Why am I seeing more RFO (Read For Ownership) requests using REP MOVSB than with vmovdqa
Your explination for why the RFO-ND optimization and 0-over-0 write elimination optimization for mutally exclusive makes sense. What I am still curious about is why
zmmfill0 seem to get worst of both worlds; being unable to make the RFO-ND optimization and having a worse rate of 0-over-0 write elimination thanymmfill0.Here is a layout of some observations that I think might be useful for figuring this out:
rep stosbwriting in 64 byte chunks is able to make the RFO-ND optimization but is not able to get the 0-over-0 write elminiation optimization.vmovdqa ymm, (reg); vmovdqa ymm, 32(reg)(assumining reg is 64 byte aligned) is unable to make the RFO-ND optimization and gets a high rate of 0-over-0 elimination optimizationvmovdqa ymm, (reg); vmovdqa ymm, 64(reg); vmovdqa ymm, 32(reg); vmovdqa ymm, 96(reg)(assumining reg is 64 byte aligned) is unable to make the RFO-ND optimization and gets a slightly higher rate of 0-over-0 elimination optimization than case 2.vmovdqa zmm, (reg)is not able to make the RFO-ND optimization and has the worse rate of 0-over-0 elminination than both case 2 and case 3 above.Case 4 is strange because it gets the worst of both worlds. Intuitively if it was the RFO-ND that prevents 0-over-0 write elimination (i.e whats happening with
rep stosb) we would either expect to see some RFO-ND requests when usingvmovdqa zmm, (reg)but we don’t. Likewise if we not seeing RFO-ND requests why would its 0-over-0 elimination rate be lower.Cases 2 and 3 I think are really interesting (reproducible by changing that order of stores here) and I might be useful in understanding case 4. The only difference between cases 2 and 3 that I can think of is that case 2 can write coalesce in the LFB whereas case 3 cannot.
So as a possible explinination for why case 3 gets a higher 0-over-0 write elimination rate than case 2 I was thinking something along the following for relationship between RFO requests and LFB coalescing.
For Case 2:
vmovdqa ymm, (reg)(write A) graduates in the store buffer and goes to LFB.vmovdqa ymm, (reg)(write B) graduates in the store buffer and goes to LFB.For Case 3:
vmovdqa ymm, (reg)(write A) graduates in the store buffer and goes to LFB.vmovdqa ymm, (reg)(write B) graduates in the store buffer and goes to LFB.(The data has the same trend with prefetched events counted)
We see here that case 2 and case 4 have basically the same RFO behavior which would indicate that writes A and B merge before the RFO request is made. What this doesn’t make clear is:
The only explination I can think of is if RFO prefetching takes place (mentioned a bit here) its possible you could try and explain the data with the following assumptions:
rep stosband why this would be case).There are basically four assumptions here any of which being untrue would blowup the theory, but if they all happened to be the case then we could explain the difference in 0-over-0 write elmination between cases 2 and 4 by saying that case 2 has many more chances to prefetch and the difference between cases 2 and 3 by saying that when case 2 fails both prefetches the coalesced RFO from writes AB will optimize out the data check.
Overall having trouble wrapping my head around all of this and wondering if you have an idea what distinguishes the 4 cases above.
Hi Noah,
Thanks for your (comprehensive!) comment.
I think RFO-ND might be a bit of a red herring here: none of the vanilla store types use this protocol, so we can mostly ignore it and treat
rep stosbas its own special thing which doesn’t get 0-over-0 optimization, and which can affect prefetchers in a totally differenet way, etc. The fact that aligned 64-bytezmmwrites don’t use the ND protocol is perhaps a bit surprising, but maybe not that surprising in that back-to-back contiguous, aligned 32-byte writes also did not use it on previous architectures and given the intermediate buffering provided by the LFB it seems like even the narrower stores could have done this, if it were easy enough. It seems like it is not easy enough.I am suprised by the
perfresults for case 3 vs the other two cases. There are more than 2x the number of RFO requests. I would have expected about the same numbers: yes, there is a lack of coalescing in the LFB (so I think performance would suffer) but I would expect ultimately that the second writes to each line would “hit” in the existing LFB or L1 (when they are allowed to proceed) and not generate any additional RFO requests.What do those numbers look like when normalized against the number of cache lines written? I.e., how many cache lines are written by the test? This helps understand which if any of the tests is close to 1:1 with lines written/RFO.
I am not sure the optimization is related to how the data is returned by the RFO. I believe it may happen much later, when the relevant lines are evicted. For instances, there is the test that initially writes non-zero values to a line, then writes zero values: in this case the optimization would not apply at the time of the RFO (non-zero values), but it would apply at the time of eviction (0s were written after, but w/o any new RFO since the lines are already locally cached in M state): in this case, I still saw the 0-over-0 optimization happen. Also, I saw it happen when the entire line is not overwritten (from my notes, although they aren’t 100% clear on this).
I believe the optimization may be load/occupancy related: e.g., only happen sometimes, when the load between some cache levels is above/below some level, or some other condition is met. In this case, small changes to the test might change things enough to affect that threshold.
Another possibility is more along the lines you mentioned: as part of the coherence flows, the “R” (data) and “O” (grant of exclusive ownership) might arrive at different times, in two different messages. Also, sometimes the outer cache might send a “pull” request to the inner cache for the data (after the inner cache indicates that it wants to write it), while other times the inner cache might send the data without a pull. Perhaps whether the optimization applies depends on the order of the messages or another detail like this and timing changes it.
Your guess that
Tested and found that
rep stosbdoes not eliminate 0 over 0 cache line stores.Hi Noah, thanks for your comment and observation about
rep stosb!I think your finding makes sense:
rep stosbcan use a “RFO-ND” (request ownership without data) protocol for larger region sizes, as opposed to vanilla RFO which brings the existing cache line up into the cache hierarchy. This works because the core can guarantee entire lines will be overwritten by the string operation since it knows the total size of the operation: thus the old data is “dead”.Since the old data isn’t fetched, it can’t be compared against zero, and a zero-over-zero optimization couldn’t happen. In essence, this RFO-ND optimization is the opposite approach to that discussed in this post: RFO-ND avoids the read implied by a store, while this zero-over-zero optimization avoids the write. I think you have to pick one or the other: I don’t see an easy way to do both for data in RAM. The RFO-ND approach has the benefit of applying to any value, not just zero.
An open question is whether the zero-over-zero optimization might apply for
rep stosbover short regions (where RFO-ND isn’t used) or if the data is already cached in L1 or L2 (since then I think the RFO-ND doens’t come into play).