I’ve added comments to my blog. You can find the existing comments, if any, and the new comment form at the bottom of any post.

I thought this would take a couple hours, but it actually took [REDACTED]. Estimates are hard.

Here’s what I did.

Table of Contents

Introduction

I am using staticman, created by Eduardo Bouças, as my comments system for this static site.

The basic flow for comment submission is as follows:

  1. A reader submits the comment form on a blog post.
  2. Javascript1 attached to the form submits it to my staticman API bridge2 running on Heroku.
  3. The API bridge does some validation of the request and submits a pull request to the github repo hosting my blog, consisting of a .yml file with the post content and meta data.
  4. When I accept the pull request, it triggers a regeneration and republishing of the content (this is a GitHub pages feature), so the reply appears almost immediately3.

Here are the detailed steps to get this working. There are several other tutorials out there, with varying states of exhaustiveness, some of which I found only after writing most of this, but I’m going to add the pile anyways. There have been several changes to deploying staticman which mean that existing resources (and this one, of course) are marked by which “era” they were written in.

The major changes are:

  • At one point the idea was that everyone would use the public staticman API bridge, but this proved unsustainable. A large amount of the work in setting up staticman is associated with running your own instance of the bridge.
  • There are three version of the staticman API: v1, v2 and v3. This guide uses v2 (although v3 is almost identical4), but the v1 version is considerably different.

Set Up GitHub Bot Account

You’ll want to create a GitHub bot account which will be the account that the API bridge uses to actually submit the pull requests to your blog repository. In principle, you can skip this step entirely and simply use your existing GitHub account, but I wouldn’t recommend it:

  • You’ll be generating a personal access token for this account, and uploading it to the cloud (Heroku) and if this somehow gets compromised, it’s better that it’s a throwaway bot account than your real account.
  • Having a dedicated account makes it easy to segregate work done by the bot, versus what you’ve done yourself. That is, you probably don’t want all the commits and pushes the bot does to show up on your personal account.

The bot account is nothing special: it is just a regular personal account that you’ll only be using from the API bridge. So, open a private browser window, go to GitHub and choose “Sign Up”. Call your bot something specific, which I’ll refer to as GITHUB-BOT-NAME from here forwards.

Generate Personal Access Token

Next, you’ll need to generate a GitHub personal access token, for your bot account. The GitHub doc does a better job of explaining this than I can. If you just want everything to work for sure now and in the future, select every single scope when it prompts you, but if you care about security you should only need the repo and user scopes (today):

Repo scope:

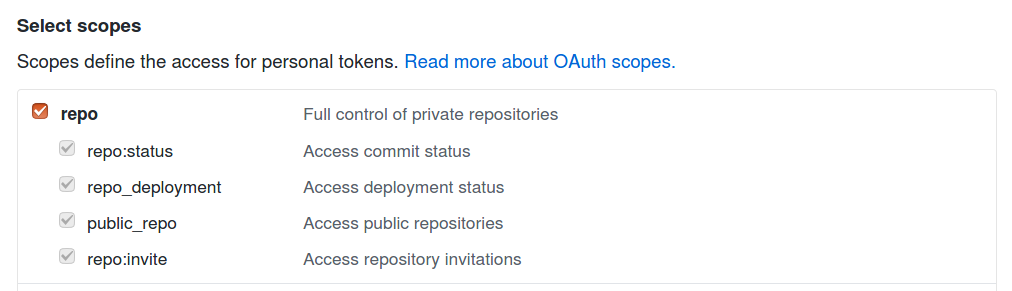
Repo scope

User scope:

User scope

Copy and paste the displayed token somewhere safe: you’ll need this token in a later step where I’ll refer to it as ${github_token}. Once you close this page there is no way to recover the access token.

Set Up the Blog Repository Configuration

You’ll need to include configuration for staticman in two separate places in your blog repository: _config.yml (the primary Jekyll config file) and staticman.yml, both at the top level of the repository.

In general, the stuff that goes in _config.yml is for use within the static generation phase of your site, e.g., controlling the generation of the comment form and the associated javascipt. The stuff in staticman.yml isn’t used during generation, but is used dynamically by the API bridge (read directly from GitHub on each request) to configure the activities of the bridge. A few thigns are duplicated in both places.

Configuring staticman.yml

Most of the configuration for the ABI bridge is set in staticman.yml which lives in the top level of your blog repository. This means that one API bridge can support many different blog repositories, each with their own configuration (indeed, this feature was critical for the original design of a shared ABI bridge).

Here’s a sample file from the staticman GitHub repository, but you might want to use this one from my repository as it is a bit more fleshed out.

The main things you want to change are shown below.


# all of these fields are nested under the comments key, which corresponds to the final element
# of the API bridge enpoint, i.e., you can different configurations even within the same staticman.yml
# file all under different keys
comments:

  # There are many more required config values here, not shown:
  # use the file linked above as a template

  # I guess used only for email notifications?
  name: "Performance Matters Blog"

  # You may want a different set of "required fields". Staticman will
  # reject posts without all of these fields
  requiredFields: ["name", "email", "message"]

  # you are going to want reCaptcha set up, but for now leave it disabled because we need the API
  # bridge up and running in order to encrypt the secrets that go in this section
  reCaptcha:
    enabled: false
  #  siteKey: 6LcWstQUAAAAALoGBcmKsgCFbMQqkiGiEt361nK1
  #  secret: a big encrypted secret (see Note above)

Configuring _config.yml

The remainder of the configuration goes in _config.yml. Here’s the configuration I added to start with (we’ll add a bit more later):

# The URL for the staticman API bridge endpoint
# You will want to modify some of the values:
#  ${github-username}: the username of the account with which you publish your blog
#  ${blog-repo}: the name of your blog repository in github
#  master: this the branch out of which your blog is published, often master or gh-pages
#  ${bridge_app_name}: the name you chose in Heroku for your bridge API
#  comments: the so-called property, this defines the key in staticman.yml where the configuration is found
#
# for me, this line reads:
# https://staticman-travisdownsio.herokuapp.com/v2/entry/travisdowns/travisdowns.github.io/master/comments
staticman_url: https://${bridge_app_name}.herokuapp.com/v2/entry/${github-username}/${blog-repo}/master/comments

Set Up the API Bridge

This section covers deploying a private instances of the API bridge to Heroku.

Generate an RSA Keypair

This keypair will be used to encrypt secrets that will be stored in public places, such as your reCAPTCHA site secret. The sececrets will be encrypted with the public half of the keypair, and decriped in the Bridge API server with the private part.

Use the following on your local to generate to generate the pair:

ssh-keygen -m PEM -t rsa -b 4096 -C "staticman key" -f ~/.ssh/staticman_key

Don’t use any passphrase5. You can change the -f argument if you want to save the key somewhere else, in which case you’ll have to use the new location when setting up the Heroku config below.

You can verify the key was genreated by running:

head -2 ~/.ssh/staticman_key

Which should output something like:

-----BEGIN RSA PRIVATE KEY-----
MIIJKAIBAAKCAgEAud7+fPWXzuxCoyyGbQTYCGi9C1N984roI/Tr7yJi074F+Cfp

Your second line will vary of course, but the first line must be -----BEGIN RSA PRIVATE KEY-----. If you see something else, perhaps mentioning OPENSSH PRIVATE KEY, it won’t work.

Sign Up for Heroku

The original idea of staticman was to have a public API bridge that everyone uses for free. However, in practice this hasn’t proved sustainable as whatever free tier the thing was running on tends to hit its limits and then the fun stops. So the current recommendation is to set up a free instance of the API bridge on Heroku. So let’s do that.

Sign up for a free account on Heroku. No credit card is required and a free account should give you enough juice for at least 1,000 comments a month6.

Deploy Staticman Bridge to Heroku

The easiest way to do this is simply to click the Deploy to Heroku button in the README on the staticman repo:

Deploy

You’ll see probably some logging indicating that the project is downloading, building and then successfully deployed.

Configure Bridge Secrets

The bridge needs a couple of secrets to do its job:

  • The GitHub personal access token of your bot account. This lets it do work on behalf of your bot account (in particular, submit pull requests to your blog repository).
  • The private key of the keypair you generated earlier.

If you want, you can add both of these through the Heroku web dashboard: go to Settings -> Reveal Config Vars, and enter them like this).

However, you might as well get familiar with the Heroku command line, because it’s pretty cool and allows you to complete this flow without having your GitHub token flow through your clipboard and makes it easy to remove the newline characters in the private key.

Follow the instructions to install and login to the Heroku CLI, then issue the following commands from any directory (note that ${github_token} is the personal access token you generated earlier: copy and paste it into the command):

heroku config:add --app ${bridge_app_name} "RSA_PRIVATE_KEY=$(cat ~/.ssh/staticman_key | tr -d '\n')"
heroku config:add --app ${bridge_app_name} "GITHUB_TOKEN=${github_token}"

Here, the tr -d '\n' part of the pipeline is removing the newlines from the private key, since Heroku config variables can’t handle them and/or the API bridge can’t handle them.

You can check that the config was correctly set by outputting it as follows:

heroku config --app ${bridge_app_name}

Invite and Accept Bot to Blog Repo

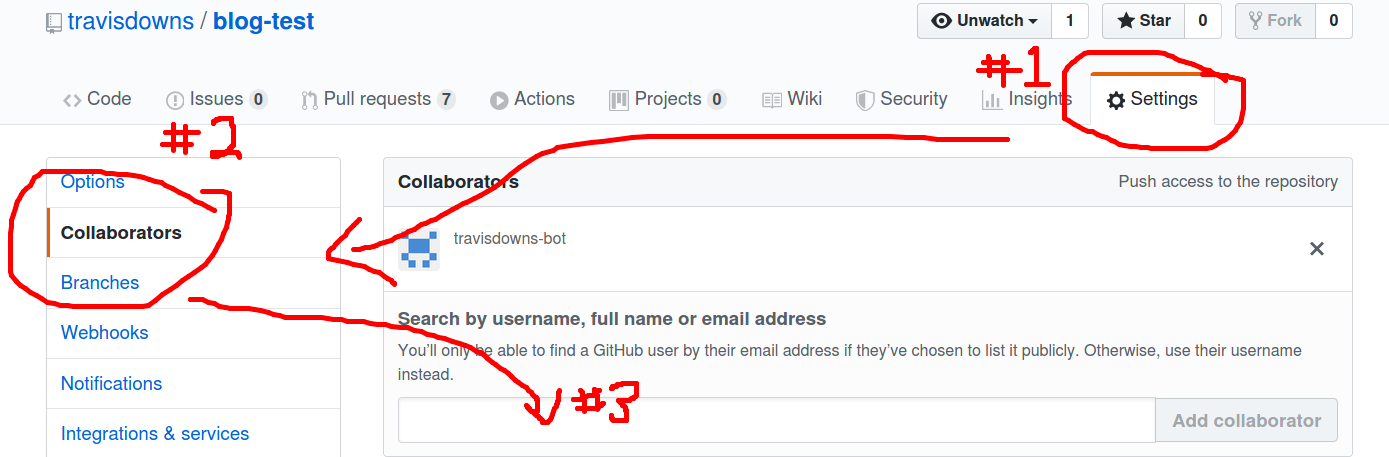
Finally, you need to invite your GitHub bot account that you created earlier to your blog repository7 and accept the invite.

Open your blog repository, go to Settings -> Collaborators and search for and add the GitHub bot account that you created earlier as a collaborator:

Adding Collaborators

Next, accept8 the invitation using the bridge API, by going to the following URL:

https://${bridge_app_name}.herokuapp.com/v2/connect/${github-username}/${blog-repo}

You should see OK! as the output if it worked: this only appears once when the invitation got accepted, at all other times it will show Invitation not found.

Enable reCAPTCHA

You are going to want to gate comment submission using reCAPTCHA or a similar system so you don’t get destroyed by spam (even if you have moderation enabled, dealing with all the pull requests will probably be tiring).

Here we’ll cover setting up reCAPTCHA, which has built-in support in staticman. Although it involves modifying the same _config.yml and staticman.yml files that we’ve modified before, this part of the configuration needs to occur after the bridge is running because we use the /encrypt endpoint on the bridge as part of the setup.

Sign Up for reCAPTCHA

Go to reCAPTCHA and sign up if you haven’t already, and create a new site. We are going to use the “v2, Checkbox” variant (docs here), although I’m interested to hear how it works out with other variants.

You will need the reCAPTCHA site key and secret key for configuration in the next section.

Configure reCAPTCHA

Next, we need to add the site key and secret key to the _config.yml and staticman.yml config files.

The site key will be used as-is, but the secret key property will be encrypted so that it is not exposed in plaintext in your configuration files. To encrypt the secret key copy the secret from the reCAPTCHA admin console, and load the following URL from your API bridge, replacing YOUR_SITE_KEY at with the copied secret key.

https://${bridge_app_name}.herokuapp.com/v2/encrypt/YOUR_SITE_KEY

You should get a blob of characters back as a result (considerably longer than the original secret) – it is this value that you need to include as reCaptcha.secret in both staticman.yml and in _config.yml.

The reCAPTCHA configuration for both files is almost the same. It looks like this for staticman.yml:

comments:

  # more stuff

  # note that reCaptcha is nested under comments
  reCaptcha:
    enabled: true
    # the siteKey is used as-is (no encryption)
    siteKey: 6LcWstQUAAAAALoGBcmKsgCFbMQqkiGiEt361nK1
    # the secret is the encrypted blob you got back from the encrypt call
    secret: a big encrypted secret (see description above)

The _config.yml version is similar except that they key appears at the top level and there is no enabled property:

# reCaptcha configuration info: the exact same site key and *encrypted* secret that you used in staticman.yml
# I personally don't think the secret needs to be included in the generated site, but the staticman API bridge uses
# it to ensure the site configuration and bridge configuration match (but why not just compare the site key?)
reCaptcha:
  siteKey: 6LcWstQUAAAAALoGBcmKsgCFbMQqkiGiEt361nK1
  secret: exactly the same secret as the staticman.yml file

Integrate Comments Into Site

Finally, you need to integrate code to display the existing comments and submit new comments.

I used a mash up of commenting code from the spinningnumbers.org blog as well as the staticman integration in the minimal mistakes theme. The advantage the former has over the latter is that the comments allow one level of nesting (replies to top-level comments are nested beneath it).

I planed to extract the associated markdown, liquid and JavaScript code to a separate repository as a single point where people could collaborate on this part of the integration, but man I’ve already spent way to long on this. I may still do it, but for now here’s how I did the integration.

Markdown Part

The key thing you need to do is include a blob of HTML and associated JavaScript in any page where you want to display and accept comments. I do this as follows:

{% if page.comments == true %}
  {% include comments.html %}
{% endif %}

You can paste it into any post, or better add it to the footer.html include or something like that (details depend on your theme). The invariant is that wherever this appears, the existing comments appear, followed by a form to submit new comments. You can see the comments.html include here – in turn, it includes comment.html (once per comment, generates the comment html) and comment_form.html which generates the new comment form.

This ultimately includes external JavaScript for JQuery and reCAPTCHA, as well as main.js which includes the JavaScript to implement the replies (moving the form when the “reply to” button is clicked, and submitting the form via AJAX to the API bridge).

You can try to use this same integration in your Jekyll blog. You’d need to:

  • Copy the _includes/comment.html, _includes/comments.html, _includes/comment_form.html, assets/main.js, and _sass/comment-styles.css from my blog files to your blog repository.
  • In assets/main.js, replace the link to https://github.com/travisdowns/travisdowns.github.io/pulls with a link to your own repository (or otherwise customize the “success” message as you see fit).
  • Include @import "comment-styles"; in your assets/main.scss file. If you don’t have one, you’ll need to create it following the rules for your theme. Usually this just means a main.scss with empty front-matter and an @import "your-theme"; line to import the theme SCSS. Alternately, you could avoid putting anything in main.scss and just include the comment styles as a separate file, but this adds another request to each post.
  • Do the include comments.html thing shown above in an appropriate place in your template/theme.
  • Set comments: true in the front matter of posts you want to have comments (or set it as a default in _config.yml).

Testing on This Post

If you want to leave a non-trivial comment on the content of this post, you can do so below. However, if you’d instead like to make a “just testing” post, to see how the http request works, or check the created pull request, etc, please do it over here. Testing only comments made on this post will be closed without accepting them.

Thanks

Thanks to Eduardo Boucas for creating staticman.

Thanks to Willy McAllister for nested comment display work I unabashedly cribbed, and helping me sort out an RSA key genreation problem, and pointing out some inconsistencies in the doc.

References

Things that were handy references while getting this working.

This comment on GitHub issue #318 was the list that I more or less follwed (I didn’t use the dev branch though).

Willy McAllister describes setting up staticman in this post – his implemented of nested comments forms the basis the one I used.

Another list of steps to get staticman working and some troubleshooting.

Michael Rose, the author of minimal mistakes Jekyll theme describes setting up nested staticman comments – I cribbed some stuff from here such as the submitting spinner.

Willy McAllister subsequently wrote a great guide to setting up Staticman, similar in nature to this one but with some additional sections such as troubleshooting and setting up reply notifications via MailGun. If that one was around when I started out, I wouldn’t have felt the need to write this one.


  1. If javascript is disabled, a regular POST action takes over. ↩

  2. I don’t think you’ll find this bridge term in the official documentation, but I’m going to use it here. ↩

  3. Well, subject to whatever edge caching GitHub pages is using – btw you can bust the cache by appending any random query parameter to the page: ...post.html?foo=1234. ↩

  4. v3 mostly just extends to the URL format for the /event endpoint to include the hosting provider (either GitHub or GitLab), allowing the use of GitHub in addition to GitLab. Almost everything in this guide would remain unchanged. ↩

  5. You could use a passphrase, but then you’ll have to change the cat used below to echo the key into the Heroku config. If you want to be super safe, best is to generate the key to a transient location like ramfs and then simply delete the private portion after you’ve uploaded it to the Heroku config. ↩

  6. In particular, the unverified (no credit card) free tier gives you 550 hours of uptime a month, and since the dyno (heroku speak for their on-demand host) sleeps after 30 minutes, I figure you can handle 550/0.5 = 1100 sparsely submitted comments. Of course, if comments come in bursts, you could handle much more than that, since you’ve already “paid” for the 30 minute uptime. ↩

  7. The bot needs to be a collaborator to, at a minimum, commit comments to the repository, and to delete branches (using the delete branches webhook which cleans up comment related branches). However, it is possible to not use either of these features if you have moderation enabled (in which case comments arrive as a PR, which doesn’t require any particular permissions), and aren’t using the webhook. So maybe you could do without the collaborator status in that case? I haven’t tested it. ↩

  8. I guess you can also just accept the invitation by opening the email sent to you by github and following the link there. This workflow involving the v2/connect endpoint probably made more sense when the API was meant to be shared among many uses using a common github bot account. ↩